Aproximaciones y errores
Cada vez que realizamos una estimación estamos aproximando el valor exacto de la medida de una magnitud a un valor cercano a él.
Vamos ahora a hacer aproximaciones de una determinada cantidad. Partimos del siguiente ejemplo:
"La marca mínima exigida a los atletas masculinos de 20 Km marcha para competir en los Juegos Olímpicos de Pekín es de 1 hora 21minutos 30 segundos."
Primero vamos a pasar esta cantidad a horas:
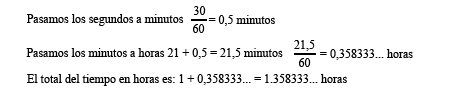
Luego 1 hora 21 minutos 30 segundos = 1,3583333... horas
El número que hemos obtenido es periódico mixto, tiene infinitas cifras decimales. Para poder trabajar con él en otras operaciones hay que "quitarle" números. Lo que hacemos es por tanto una aproximación. La aproximación será más exacta cuando ésta se acerque más al valor real.
¿Cómo eliminamos los números? Esto no se hace de cualquier manera. Utilizamos lo que se denomina redondeo:
- Si la cifra que vamos a eliminar es mayor o igual que 5, sumamos 1 a la cifra anterior.
- Si la cifra es menor que 5, la cifra anterior se queda como está.
Vamos a aproximar el tiempo de 1,3583333...horas. Dependiendo del número de decimales que dejemos así será la aproximación: diezmilésimas 4 decimales, milésimas 3, centésimas 2, décimas 1.
| Aproximación a | Unidad | Décimas | Centésimas | Milésimas | Diezmilésimas | Número |
| Diezmilésimas | 1 | 3 | 5 | 8 | 3 | 1,3583 |
| Milésimas | 1 | 3 | 5 | 8 | 1,358 | |
| Centésimas | 1 | 3 | 5 + 1 = 6 | 1,36 | ||
| Décimas | 1 | 3 + 1= 4 | 1,4 |
Se llaman cifras significativas a aquellas que expresan el valor de la medida realizada. Está medida deberá venir acompañada de su correspondiente unidad.
El número de cifras significativas dependerá de la exactitud con la que se necesite dar el resultado; por ejemplo, si medimos el tiempo de los atletas de la maratón, éste vendrá dado en horas, minutos y segundos. En cambio, en las marcas de los atletas de velocidad se necesita precisar hasta las centésimas de segundo. Se necesitan más cifras significativas.
Cuando el valor de una medida se haya calculado con una fórmula matemática, el resultado no se da con todas las cifras que nos proporciona la calculadora, sino que se expresa con el mismo número de cifras que la medida que menos tenga.
¿Cómo cuantificar el error que se está cometiendo al aproximar?
Cada vez que estimamos o aproximamos una medida estamos cometiendo errores. Cuánto más pequeño sea el error cometido en nuestra medida mejor será ésta.
Llamamos error absoluto de una medida a la diferencia en valor absoluto que hay entre el valor exacto y el valor aproximado de dicha medida. Recuerda, el valor absoluto nos dice que esta cantidad es siempre positiva.
¿De cuánto es el error que se comete en las aproximaciones del ejemplo anterior?
| Aproximación a | Valor aproximado | |Valorreal - Valoraproximado| | Error absoluto |
| Diezmilésimas | 1,3583 | 0,000033... | |
| Milésimas | 1,358 | 0,000333... | |
| Centésimas | 1,36 | 0,001666... | |
| Décimas | 1,4 | 0,041666... |
A medida que disminuye el número de cifras decimales, el error que se va cometiendo es mayor y por tanto la medida que estamos utilizando será menos exacta.
Vamos ahora con otro ejemplo: supongamos que dos personas miden la misma estantería. ¿El resultado de la medida será el mismo? Probablemente no: el punto inicial y final donde colocamos el metro no será el mismo, por lo que el resultado será diferente. Pero además, dependerá del metro que cada uno estemos utilizando.
Imaginemos que estamos midiendo la longitud de una estantería con un metro que tiene un error de medida de 0,2 cm (no sabemos en principio si de más o de menos). ¿Qué significa esto?
Significa que si nosotros hemos medido 100 cm, la medida real no tiene por qué ser 100 cm.
- Si hacemos una aproximación por defecto la longitud de la estantería será:
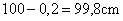
- Si hacemos una aproximación por exceso la longitud de la estantería será:
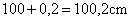
La medida real de nuestra estantería es un valor que está entre 99,8 y 100,2 cm.
Una medida siempre es aproximada debido a las limitaciones del procedimiento seguido y a las del instrumento que estamos empleando.