Identificación de magnitudes directa e inversamente proporcionales
Cuando aplicamos estos conceptos a las magnitudes físicas, la relación entre ellas se denomina constante de proporcionalidad (k).
Podemos encontrarnos con dos situaciones:
Cuando la constante de proporcionalidad coincide con la razón, es decir, si;
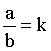
Siendo k dicha constante, quiere decir que "a" tiene siempre un valor igual a:
"
"
En este caso, "a" y "b", serían magnitudes directamente proporcionales, esto es, si "b" aumenta, "a" aumenta proporcionalmente un valor "k.b", y si "b" disminuye, "a" disminuye proporcionalmente, de la misma manera.
Cuando el producto de dos magnitudes es igual a la constante de proporcionalidad, es decir:
En este caso, "a" y "b", serían magnitudes inversamente proporcionales, porque cuando una aumenta, la otra disminuye, y viceversa, aunque siempre en la misma proporción.
Si  ,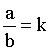
"a" y "b" son magnitudes directamente proporcionales.
|
inversamente proporcionales. |
,
"a" y "b" son magnitudesVeamos esto con unos ejemplos:
Ejemplo 1
Para un movimiento rectilíneo uniforme, es decir con una trayectoria recta, y con velocidad constante, nos dan los siguientes datos:
El conductor ha tardado 5 s en recorrer 50 metros, 10 s en recorrer 100 m, 20 s en recorrer 200 m... Evidentemente, el espacio y el tiempo, son magnitudes directamente proporcionales. Lo comprobamos a continuación.
Para ver la proporcionalidad entre los espacios y los tiempos, utilizamos la expresión:
= k: 
= k 
= 
= 
=
10
k = 10.
El valor de la constante de proporcionalidad es 10, que es precisamente, el valor constante de la velocidad del movimiento, cuya expresión matemática para este tipo de movimientos es: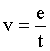 
.
Ejemplo 2
Cuando aplicamos una fuerza "F" sobre una superficie determinada, "S", ejercemos una presión "P", que viene dada por la expresión:
Vamos a mantener la fuerza constante, para ver la relación entre la presión y la superficie.
Supongamos que aplicamos una fuerza de 0,5 Newton para clavar un clavo en la pared. Si la superficie del clavo es grande, la presión ejercida será menor, pero si cogemos un clavo con menor superficie, aplicando la misma fuerza, penetrará más fácilmente en la pared, porque la presión será más grande.
Supongamos ahora que un niño de 25 Kg (250 N de peso), está sobre la nieve con botas. Si la nieve está blanda el niño se hundirá. Para evitar esto, se coloca los esquís. En este caso no se hunde, porque la superficie sobre la que se ejerce la fuerza, que es el peso del niño, es mucho mayor, ya que el área de los esquís es muy superior a la de la suelas de las botas.
Hechos como estos nos demuestran que a mayor superficie menor presión, y viceversa. Por lo tanto, presión y superficie son magnitudes inversamente proporcionales, lo cual está de a cuerdo con la definición vista anteriormente:
Que se ajusta a la definición de magnitudes inversamente proporcionales:
 |
 |